Introduction
Resolution in fluorescence microscopy is defined as the shortest distance between two points on a specimen that can still be distinguished. This is primarily determined by two factors; microscope resolution, which is the smallest object the microscope can resolve, and camera resolution, which is the ability of the camera to detect what the microscope can resolve.
The maximum resolution of the microscope is a function of the numerical aperture of the objective lens and the emission wavelength of the sample, whereas camera resolution is determined entirely by pixel size.
However, the resolving power of a fluorescence microscope is ultimately restricted by the diffraction limit of light which, when using green light (510 nm) for example, would be around 220 nm. This sets a lower limit on what can be resolved. It is therefore common practice in standard fluorescence microscopy to use a microscope setup capable of reaching this lower limit to detect the smallest resolvable object. Attempting to resolve lower than this isn’t possible using conventional microscopy, it’s only possible to break the diffraction limit of light using super-resolution techniques.
Microscope Resolution
Light travels as a wave so when it is focused to a small spot with a lens, no matter how good the objective lens is, the focal spot will have a larger size than the actual fluorophore.
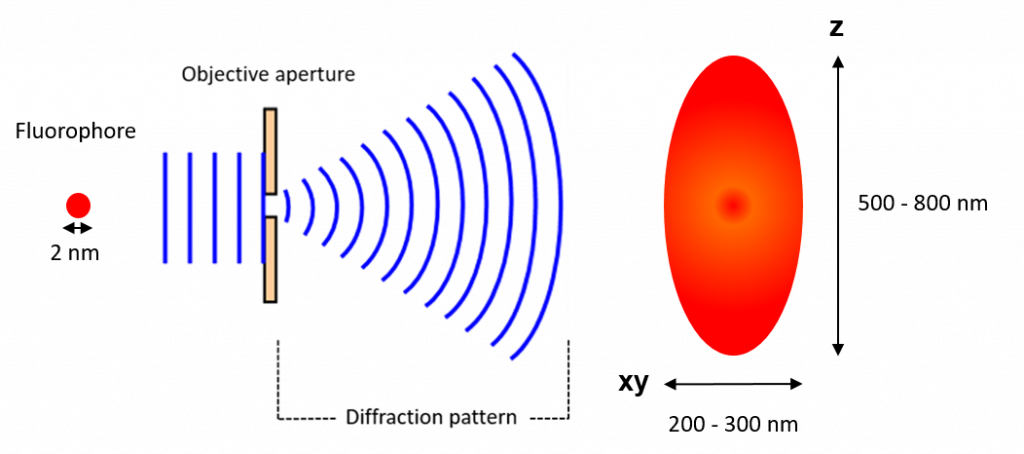
This happens because the wavefront of the fluorescence emission becomes diffracted at the edges of the objective aperture. This effectively spreads the
wavefront out, widening the fluorescence emission into a diffraction pattern which has a central spot larger than the original fluorophore (Figure 1).
The size of the diffraction limited spot is approximately half the size of the wavelength of light emitted but the full equation, determined by Ernst Abbe in 1873, is:
𝑑 = 𝜆 / 2NA
Where d is the size of the diffraction limited spot, λ is the wavelength of light used and 2NA is 2 times the numerical aperture of the objective.
In the case of GFP, which emits at ~510 nm, and a high (NA 1.4) numerical aperture objective, the size of the fluorophore as resolved by the microscope would be 182 nm. This is much larger than the actual fluorophore which may be just 2 nm.
Airy Disks
The diffraction limited spot takes the shape of an Airy disk (Figure 2), named after George Biddell Airy. It consists of a bright central spot with a series of diffraction rings surrounding it. The size of the central spot is determined by the wavelength of light being emitted and the numerical aperture of the objective.
Figure 2 highlights how increasing the numerical aperture of the objective lens reduces the size of the Airy disk and therefore increases the amount of resolvable detail.

The Rayleigh Criterion
The issue with resolving adjacent fluorophores is that as Airy disks move closer together they merge with one another and become unresolvable (Figure 3). Thus, in 1896, Lord Rayleigh refined the Abbe equation to take into account how far apart two fluorophores need to be to differentiate them:
𝑑 = 1.22𝜆 / 2NA
With this refinement, the distance required to differentiate two GFP fluorophores with a high (NA 1.4) objective would be 222 nm.

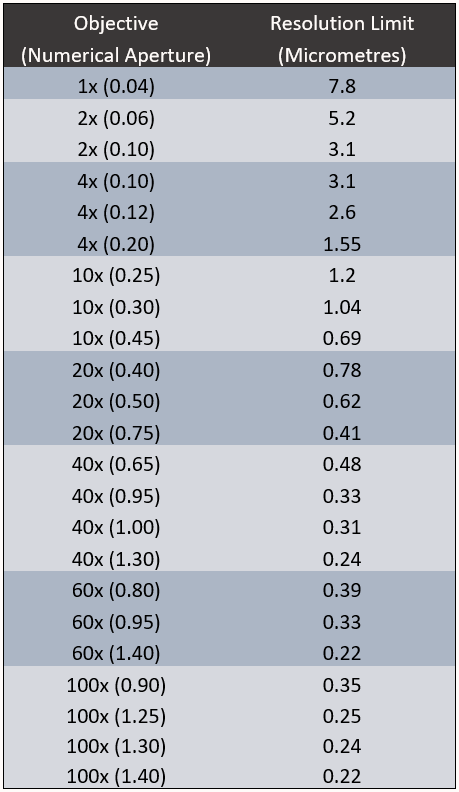
Resolution Limit Of Objectives
The information in Table 1 highlights the resolution limit possible with a variety of different magnification objectives and numerical apertures using GFP (510 nm) emission.
It’s important to note that objective magnification has no impact on resolution, numerical aperture is the only important value. A 100x, 1.40 NA objective has the same resolving power as a 60x, 1.40 NA objective. Equally, a 100x, 1.30 NA objective has the same resolving power as a 40x, 1.30 NA objective.
This leads to the obvious question, why use 100x or 60x magnification if 40x magnification achieves the same resolution? When using higher magnification objectives, field of view is being restricted for no reason.
By using lower magnification objectives, changing from a 100x, 1.30 NA objective to a 40x, 1.30 NA objective, field of view is increased by 450%. That represents a 450% increase in sample area with no loss in resolution.
Equally, by changing from a 60x, 1.30 NA objective to a 40x, 1.30 NA objective, sample area is increased by 200%.
So why use higher magnification objectives at all? This is where camera resolution comes in. Magnification plays a big part in the resolving power of a scientific camera.
Camera Resolution
Camera resolution is defined as the ability of the camera sensor to sample the image and the resolving power of a scientific camera is entirely dependent on the size of the pixel and by how much it is magnified. Figure 4 highlights how scientific camera pixel size is changed by objective magnification.

6.5 μm pixels reduced in size by a 10x objective result in an effective pixel size of 0.65 μm, a 40x objective results in an effective pixel size of 0.1625 μm and a 60x objective results in an effective pixel size of 0.108 μm
The most obvious way to match camera resolution to microscope resolution would appear to be simply matching the diffraction-limited resolution given in Table 1 to the size of a single pixel. However, this is not the case. The goal isn’t just to match the microscope resolution but to distinguish adjacent objects.
Nyquist Sampling
As Figure 5 illustrates, if microscope resolution is matched to the size of a single pixel, then it is possible that two adjacent objects could be imaged onto adjacent pixels. In this case, there would be no way of discerning them as two separate objects in the resulting image.
Separating adjacent features requires the presence of at least one intervening pixel with a different intensity value. For this reason, the best spatial resolution that can be achieved requires matching the diffraction-limited resolution of the microscope to two pixels on the sensor. This is called Nyquist sampling and it can be calculated using the equation:
Camera Resolution = (Pixel Size / Objective Power) x 2.3

Matching Camera Resolution To Microscope Resolution
The pixel size required to achieve Nyquist sampling at different magnifications is illustrated in Tables 2 and 3. These tables provide the answer to the question posed before: Why use 100x or 60x magnification if 40x magnification achieves the same resolution?
As discussed previously, to achieve Nyquist sampling and match the microscope resolution using GFP (510 nm), the camera resolution should reach 0.22 μm. Table 2 shows that for a 40x objective, a 6.5 μm pixel is too large as the resulting camera resolution is 0.37 μm. A 6.5 μm pixel is considered sufficient for 60x magnification, however, as the resulting camera resolution reaches 0.25 μm.
A smaller pixel is therefore required to achieve Nyquist sampling at 40x. Table 3 shows that a smaller pixel size of 4.25 μm reaches a camera resolution of 0.24 μm with 40x magnification which satisfies Nyquist.


The data presented in this section illustrates that the lowest magnification that can be used is limited by the pixel size of the camera, which needs to be small enough to match the microscope resolution.
A smaller pixel camera allows for a lower magnification to be used which has the advantage of seeing more of the sample in the field of view.
Summary
There are two types of resolution; microscope resolution and camera resolution. Microscope resolution is determined by the numerical aperture of the objective and the emission wavelength whereas camera resolution is determined by pixel size.
It’s possible to reach diffraction-limited resolution with lower (40x) magnification objectives but pixel size becomes limiting. To remedy this, cameras have been developed with smaller pixels to allow researchers to move to lower magnification objectives. This has the advantage of increasing the field of view without sacrificing resolution. Researchers can expect to increase throughput 200% just by switching from 60x to 40x.
