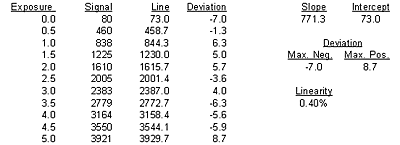
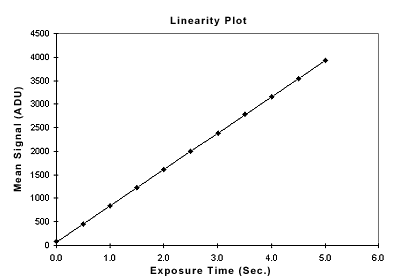
Linearity
The fundamental process that occurs in CCD imaging is the conversion of photonic input to electronic output. Photons incident on the CCD will be converted to electron/hole pairs and the electrons will be captured under the gate electrodes of the CCD. These electrons are then transferred in a “bucket brigade” fashion to the output amplifier where the charge is converted to a voltage output signal. An analog processing chain further amplifies this signal and finally it is digitized before being transferred to a host computer for display, image processing, and/or storage. The transfer function between the incident photonic signal and the final digitized output should vary linearly with the amount of light incident on the CCD. Hence, nonlinearity is a measure of the deviation from the following relationship:
Digital Signal = Constant x Amount of Incident Light
High-performance CCD cameras have extremely good linearity. Deviations from linearity are often less than a few tenths of a percent for over five orders of magnitude. This is far superior to video CCDs and other solid-state imagers, which can exhibit nonlinearity of several percent or more. For quantitative imaging, linearity is a stringent requirement. CCDs must be linear in order to perform image analysis such as arithmetic ratios, shading correction, flat fielding, linear transforms, etc.
There is no standard method for measuring or reporting linearity values. Typically the numbers are reported as percent deviations from linearity (it may be specified as linearity or nonlinearity, however).
One method that can be used is to plot the mean signal value versus the exposure time over the full linear range (linear full well) of the CCD. A linear least-squares regression can then be fit to the data. The deviation of each point from the calculated line gives a measure of the nonlinearity of the system. The nonlinearity can be reported as the sum of the maximum and minimum deviation divided by the maximum signal as a percentage: